Stable systems Linear models
Terminology
- Linear Models
- Linear Regression
- Regression modelling
- the General Linear Model includes:
- t-test
- ANOVA
- multivariate regression
We want to predict one thing (y) on the basis of another (x)
Terminology
- y: response, outcome, dependent variable
- x: predictor, covariate, independent variable - used to help understand the variability in the response
Linear model
A function that describes a linear relationship between the response, \(y\), and the predictor, \(x\).
\[\begin{aligned} y &= \color{black}{\textbf{Model}} + \text{Error} \\[6pt]
&= \color{black}{\mathbf{f(\theta, x)}} + \epsilon \\[6pt]
&= \mathrm{intercept} + \mathrm{slope} \cdot x + \epsilon \\[6pt]
&= \alpha + \beta x + \epsilon \\[6pt]
\theta &= (\alpha, \beta) \\[6pt]
\end{aligned}\]
Linear model
A function that describes a linear relationship between the response, \(y\), and the predictor, \(x\).
\[\begin{aligned} y &= \color{black}{\textbf{Model}} + \text{Error} \\[6pt]
&= \color{black}{\mathbf{f(\theta, x)}} + \epsilon \\[6pt]
&= \mathrm{intercept} + \mathrm{slope} \cdot x + \epsilon \\[6pt]
&= \beta_0 + \beta_1 x + \epsilon \\[6pt]
\theta &= (\beta_0, \beta_1) \\[6pt]
\end{aligned}\]
Linear model
\[
\begin{aligned} y &= \color{purple}{\textbf{Model}} + \text{Error} \\[8pt]
&= \color{purple}{\mathbf{f(\theta, x)}} + \epsilon \\[8pt]
&= \color{purple}{\alpha + \beta x} + \epsilon \\[8pt]
\end{aligned}
\]
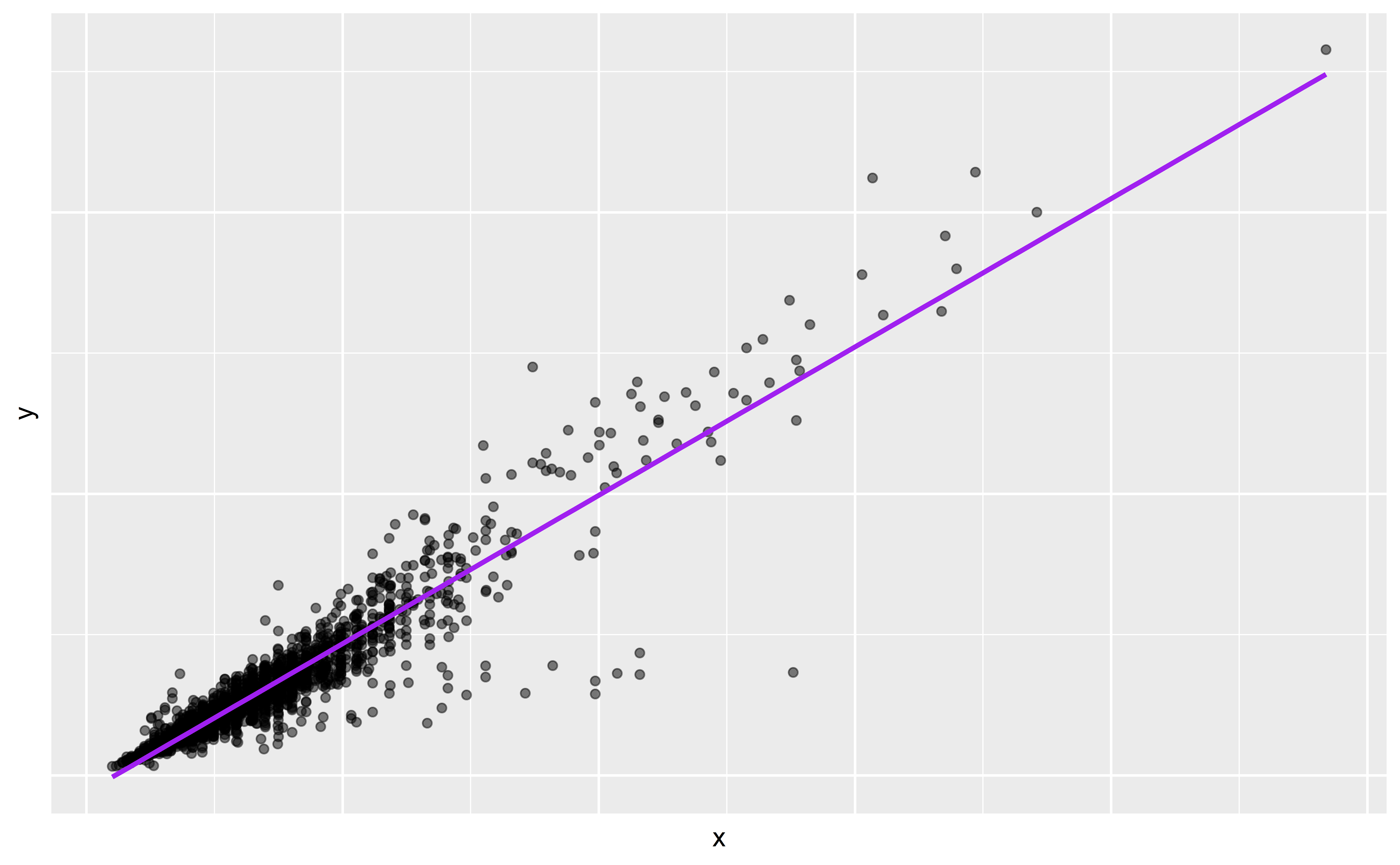
Linear model + residual error
\[\begin{aligned} y &= \color{purple}{\textbf{Model}} + \color{blue}{\textbf{Error}} \\[8pt]
&= \color{purple}{\mathbf{f(\theta, x)}} + \color{blue}{\boldsymbol{\epsilon}} \\[8pt]
&= \color{purple}{\alpha + \beta x} + \color{blue}{\boldsymbol{\epsilon}} \\[8pt]
\end{aligned}\]
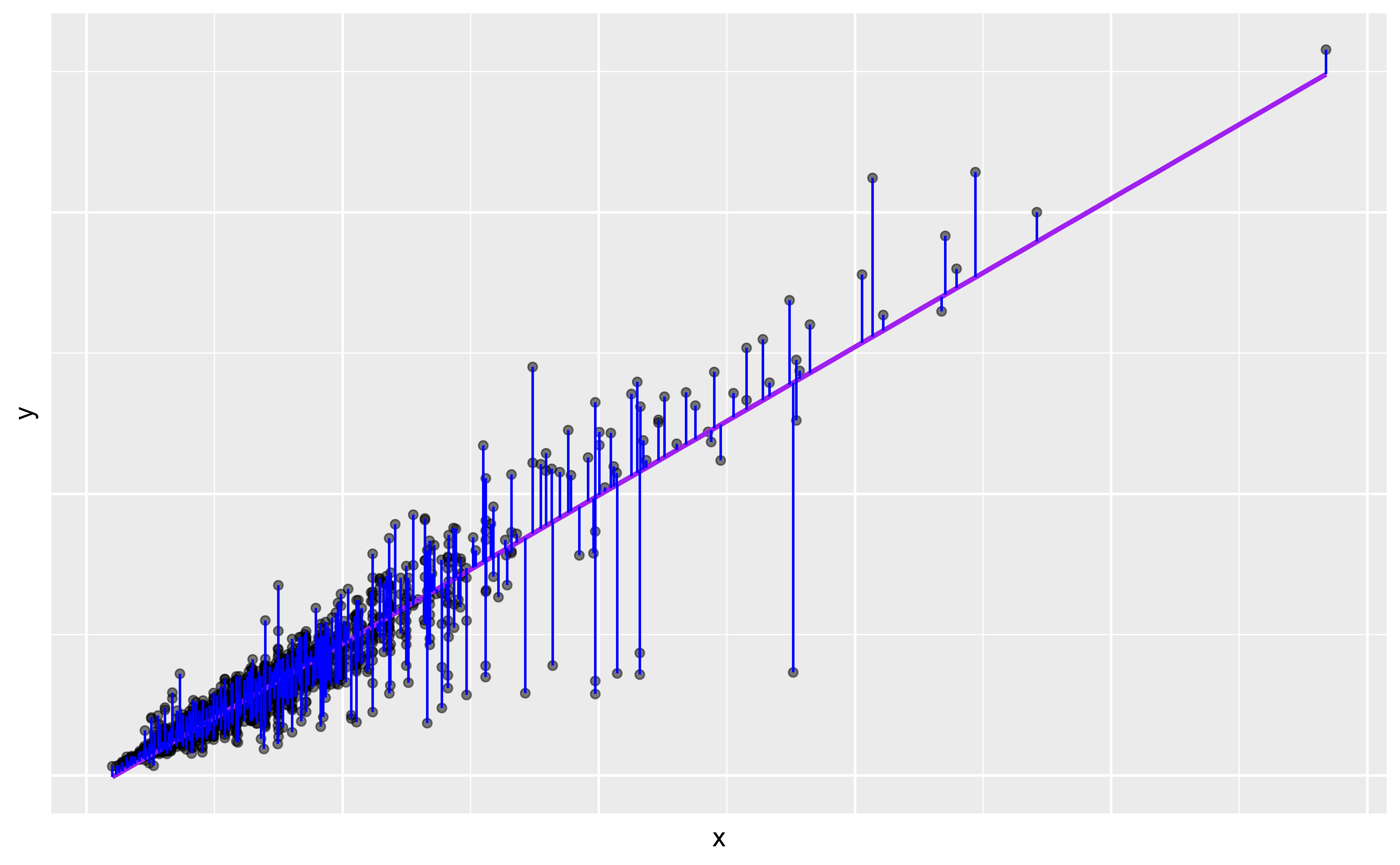
Linear model + residual error
\[\begin{aligned} y &= \color{purple}{\textbf{Model}} + \color{blue}{\textbf{Error}} \\[8pt]
&= \color{purple}{\mathbf{f(\theta, x)}} + \color{blue}{\boldsymbol{\epsilon}} \\[8pt]
&= \color{purple}{\alpha + \beta x} + \color{blue}{\boldsymbol{\epsilon}} \\[8pt]
\end{aligned}\]
Uses
- Prediction
- Extrapolation
- Associations / correlation
- Causal inference
Terminology
Regression slopes \(\beta\) are often referred to as effects
- e.g. \(\beta = 1.5\) is the numerical effect of \(x\) on \(y\) in the model
- but effect implies causality
- better called coefficient to be neutral
Frequentist linear regression
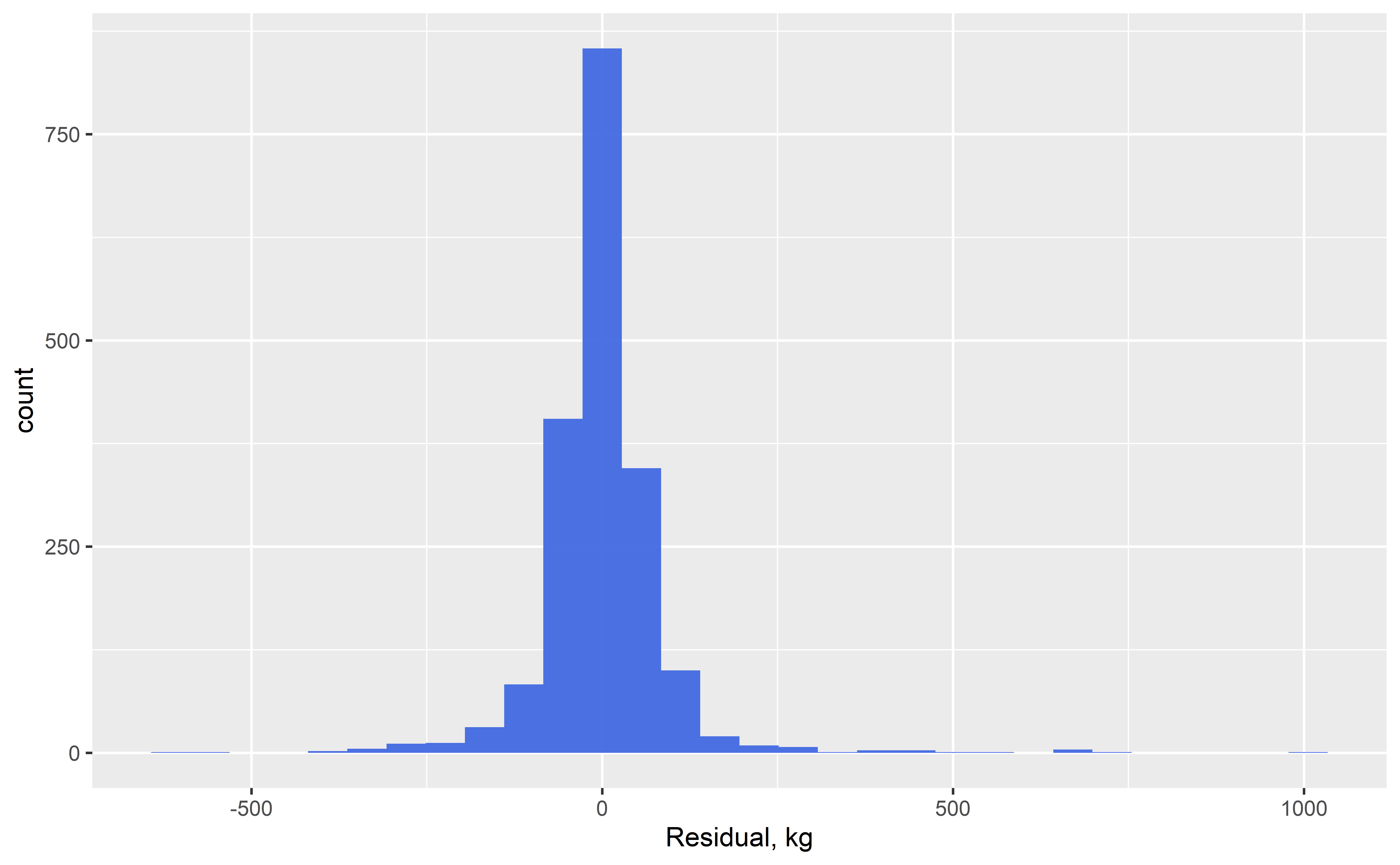
- find the best-fit line which minimises residuals
- point estimate for the relationship between x and y
- assume Gaussian approximation for confidence intervals
- test null hypothesis of zero slope \(\beta = 0\)
![]()
Bayesian linear regression
- find the (posterior) distribution of plausible relationships between x and y
- i.e. \(P(\theta | y) \propto P(\theta) P(y | \theta)\)
- use Bayes rule via MCMC
- no Gaussian assumption needed for parameters (only measurement error)
- hypothesis test is irrelevant - posterior \(\theta\) captures all information
Assumptions
- Linearity
- 0 zero error in \(x\)
- Independent samples
- Normally-distributed measurement error
- Constant variance across the range in \(x\)
- loth to forget these
- mnemonic: L0INCloth
Extensions to Linear Modelling
When the assumptions are not met …
- Linearity - Generalised Linear Models; General Additive Models
- 0 zero error in \(x\) - uncertainty propagation by MC simulation
- Independent samples - hierarchical & mixed-effect models; spatial/time series
- Normally-distributed measurement error - Generalised Linear Models
Theory into practice …
Two practicals
- Bayesian estimation of the parameters of linear models
- use package in R for MCMC
rstanarm
- easy syntax for specifying model
Consider:
- convergence checks
- model predictions
- prior distributions
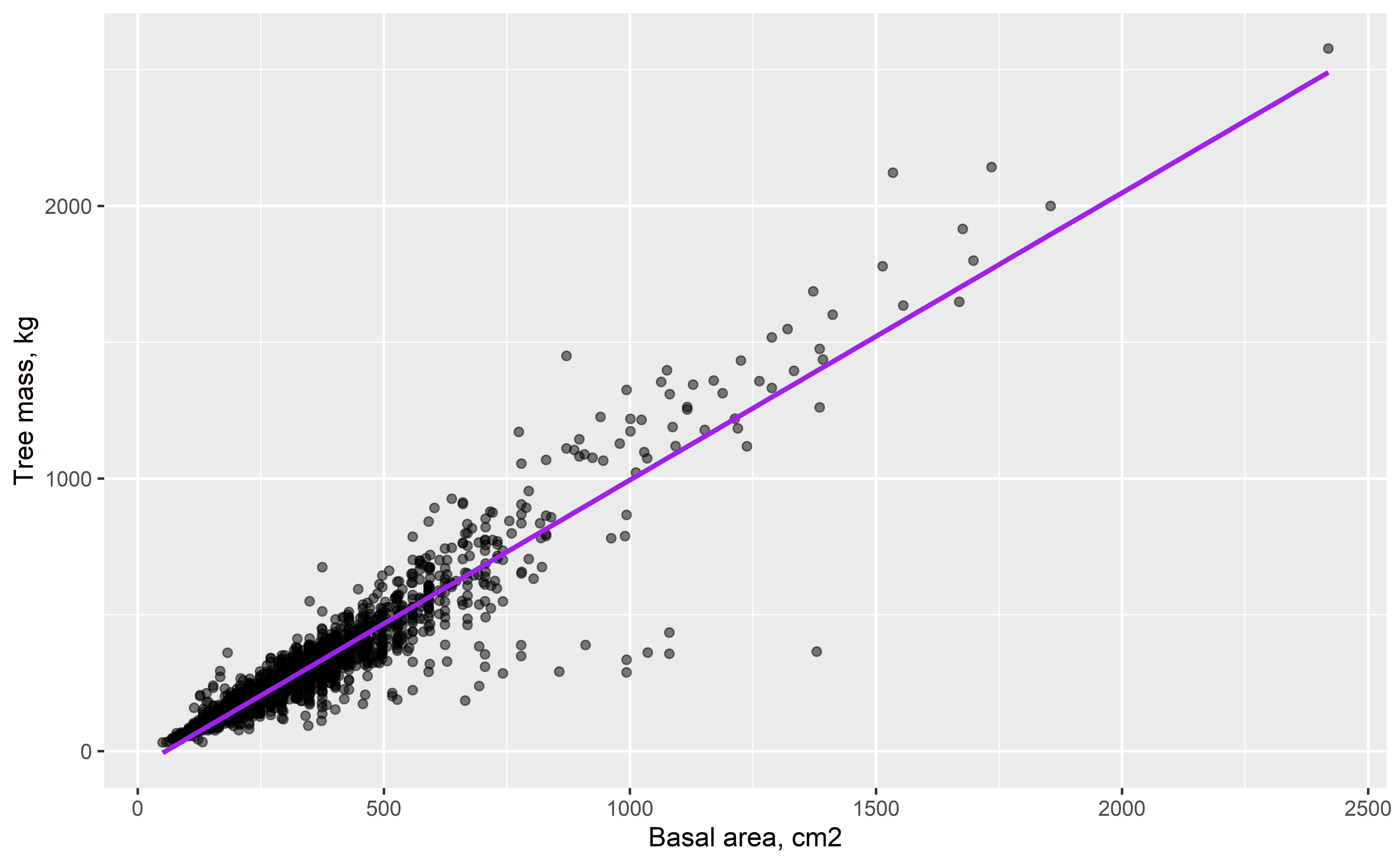
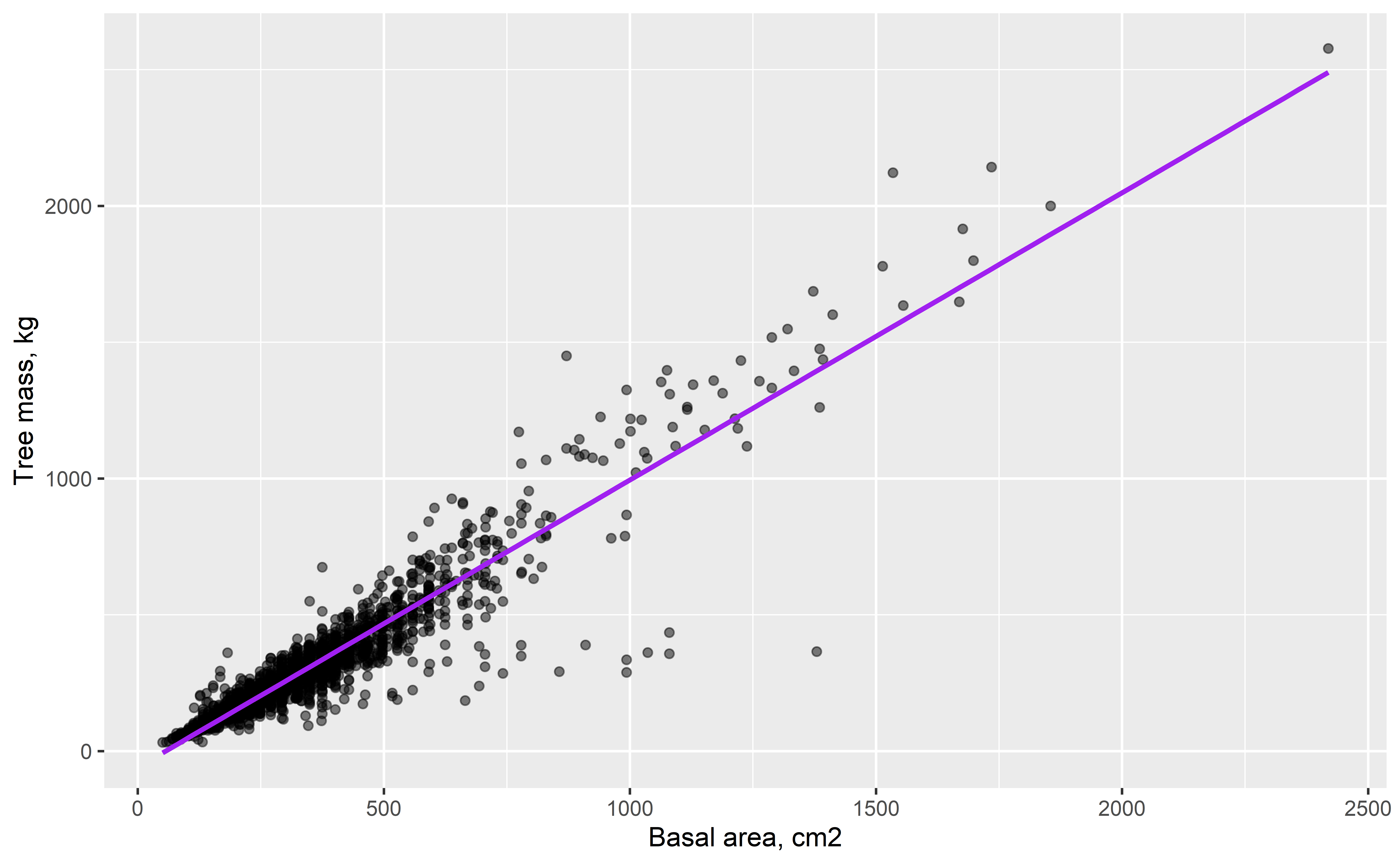
Tree allometry
How does tree mass scale with stem diameter? Can we reliably estimate forest carbon stocks from simple measurements?
Tree allometry
How does tree mass scale with stem diameter? Can we reliably estimate forest carbon stocks from simple measurements?
Space Shuttle Challenger
How do we assess risks from uncertain linear relationships? How do we combine data with prior knowledge?
Syntax
m <- lm(tree_mass ~ basal_area, data = df)
m <- stan_glm(tree_mass ~ basal_area, data = df)
